Linear Regression using Scikit-learn
Machine Learning: Field of study that gives computers the ability to learn without being explicitly programmed. – Arthur Samuel (1959)
Machine learning is an application of Artificial Intelligence (AI). The focus of machine learning is to train algorithms to learn patterns and make predictions from data. Machine learning is especially valuable because it lets us use computers to automate decision-making processes.
Netflix and Amazon use machine learning to make new product recommendations. Banks use machine learning to detect fraudulent activity in credit card. Healthcare industry is making use of machine learning to detect diseases and to montor and assess patients.
Linear Regression
Linear Regression is a supervised learning problem where the answer to be learned is a continuous value. Linear regression is used to predict the value of an outcome variable Y based on one or more input predictor variables X. The aim is to establish a linear relationship (a mathematical formula) between the predictor variable(s) and the response variable, so that, we can use this formula to estimate the value of the response Y, when only the predictors (Xs) values are known.
In this tutorial, we will implement a simple linear regression algorithm in Python using Scikit-learn, a machine learning tool for Python.
Loading the dataset.
The dataset that we will use will help us in determining if there is a relation between Brain weight(grams) and Head size(cubic cm). The data set is associated with the following paper: A Study of the Relations of the Brain to to the Size of the Head, by R.J. Gladstone, published in Biometrika, 1905. It’s a rather quaint data set, created well over a century ago and can be downloaded from here.
1
2
3
4
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
1
2
df = pd.read_csv('dataset_brain.txt', comment='#', sep='\s+')
df.head()
| gender | age-group | head-size | brain-weight | |
|---|---|---|---|---|
| 0 | 1 | 1 | 4512 | 1530 |
| 1 | 1 | 1 | 3738 | 1297 |
| 2 | 1 | 1 | 4261 | 1335 |
| 3 | 1 | 1 | 3777 | 1282 |
| 4 | 1 | 1 | 4177 | 1590 |
Visualizing data
1
2
3
plt.scatter(df['head-size'], df['brain-weight'])
plt.xlabel('Head size (cm^3)')
plt.ylabel('Brain weight (grams)');
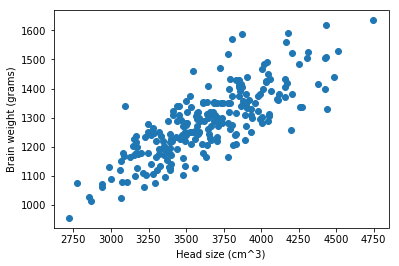
Preparing the data
1
2
y = df['brain-weight'].values
y.shape
(237,)
1
2
3
X = df['head-size'].values
X = X.reshape(X.shape[0], 1)
X.shape
(237, 1)
A general practice is to split your data into a training and test set. You train/tune your model with your training set and test how well it generalizes to data it has never seen before with your test set. We will make use of scikit learn’s train_test_split method to achieve this.
1
2
3
4
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=100)
Let us visualize the training and test set data.
1
2
3
4
plt.scatter(X_train, y_train, c='blue', marker='o')
plt.scatter(X_test, y_test, c='red', marker='p')
plt.xlabel('Head size (cm^3)')
plt.ylabel('Brain weight (grams)');
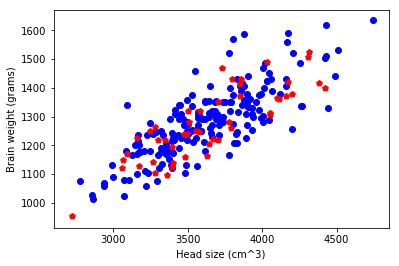
Training the Model
1
2
3
4
5
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X_train, y_train)
y_pred = lr.predict(X_test)
Evaluating the model
is a statistical measure of how close the data are to the fitted regression line. It is also known as the coefficient of determination.
In general, the higher the R-squared, the better the model fits your data. Scikit learn’s score function returns the coefficient of determination of the prediction.
1
lr.score(X_test, y_test)
0.68879769950865688
Let us also plot the regression line which will help us in giving a better intuition about Linear Regression.
1
2
3
4
5
6
7
8
9
10
min_pred = X_train.min() * lr.coef_ + lr.intercept_
max_pred = X_train.max() * lr.coef_ + lr.intercept_
plt.scatter(X_train, y_train, c='blue', marker='o')
plt.plot([X_train.min(), X_train.max()],
[min_pred, max_pred],
color='red',
linewidth=4)
plt.xlabel('Head size (cm^3)')
plt.ylabel('Brain weight (grams)');
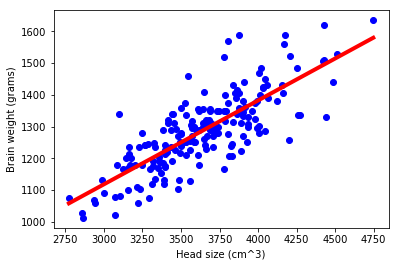
Entire code is available on github.
To know more about Linear Regression check out this link.
